Friday, March 31, 2017
Thursday, March 23, 2017
Sunday, March 19, 2017
Saturday, March 18, 2017
Wednesday, March 15, 2017
Tuesday, March 14, 2017
Saturday, March 11, 2017
Sunday, March 5, 2017
Saturday, March 4, 2017
Worksheet class 9 chapter 8 quadrilaterals
Chapter - 8
(Quadrilaterals)
Key Concept
(1) Sum of the angles of a quadrilateral is 3600.
(2) A diagonals of a parallelogram divides it into two congruent triangles.
(3) In a parallelogram
(a) diagonals bisects each other.
(b) opposite angles are equal.
(c) opposite sides are equal
(4) Diagonals of a square bisects each other at right angles and are equal, and vice-
versa.
(5) A line through the mid-point of a side of a triangle parallel to another side bisects
the third side. (Mid point theorem)
(6) The line through the mid points of sides of a ∆║ to third side and half of it.
Section - A
Q.1 The figures obtained by joining the mid-points of the sides of a rhombus, taken in
order, is
(a) a square (b) a rhombus
(c) a parallelogram (d) a rectangle
Q.2 The diagonals AC and BD of a parallelogram ABCD intersect each other at the
point O, if ∟DAC = 320 and ∟AOB = 720
then ∟DBC is
(a) 320 (b) 240 (c) 400 (d) 630
Q.3 In a square ABCD, the diagonals AC and BD bisect at 0. Then ∆AOB is
(a) acute angled (b) right angled
(c) obtuse angled (d) equilateral
Q.4 ABCD is a rhombus such that ∟ACB = 400 then ∟ADB is
(a) 400 (b) 450 (c) 500 (d) 600
Q.5 A quadrilateral ABCD is a parallelogram if
(a) AD || BC (b) AB = CD
(c) AB = AD (d) ∟A = 600, ∟C =
600, ∟B = 1200
Q.6 Three angles of a quadrilateral are 600, 700 and 800. The fourth angle is
(a) 1500 (b) 1600 (c) 1400 (d) None of these
Section - B
Q.7 In the adjoining figure QR=RS
Find
Q.8 Prove that the sum of the four angles of a quadrilateral is 3600.
Q.9 Prove that the diagonals of a parallelogram bisects each other.
Q.10 The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the
quadrilateral.
Q.11 ABCD is a rectangle in which diagonal AC bisects ∟A as well as ∟C. Show that
ABCD is a square
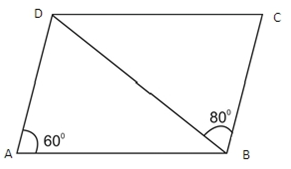
Q.12 In the adjoining figure, ABCD is a ||gm. If ∟DAB = 600 and ∟DBC = 800 .
Find
∟CDB and ∟ADB.
Section - C
Q.13 Prove that the line segment joining the mid-points of two sides of a triangle is
parallel to the third side.
Q.14 ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD
and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Q.15 Prove that the straight line joining the mid-points of the diagonals of a trapezium
is parallel to the parallel sides and is equal to half their difference.
Q.16 In the adjoining figure, D, E and F are mid-points of the sides BC, CA and AB of ∆ABC If AB = 4.3cm, BC = 5.6cm and AC = 3.5cm, find the perimeter of ∆EFD
Q.17 In a parallelogram ABCD, AP and CQ are drawn perpendiculars from vertices A
and C on diagonal BD. Prove that
Q.18 In a parallelogram ABCD, E and F are points on AB and CD such that AE = CE.
Prove that ED||BF.
Section - D
Q.19 If a line is parallel to the base of a trapezium and bisects one of the non-parallel
sides, then prove that it bisects either diagonal of the trapezium.
Q.20 AD is a median of
∆ABC and E is the mid-point of AD. BE Produced meets AC in
F. Prove that
AF = 1/3 AC.
Q.21 ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse
AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) CM =
MA = 1/2AB.
Q.22 Show that the bisectors of angles of a parallelogram form a rectangle.
Answers -
Q.1 (d) Rectangle
Q,2 (c) 400
Q.3 (b) Right angled
Q.4 (c) 500
Q.5 (d) ∟A = 600, ∟C = 600 , ∟B = 1200
Q.6 (a) 1500
Q. 7 ∟PSR = 1050
Subscribe to:
Posts (Atom)