Chapter - 8
(Quadrilaterals)
Key Concept
(1) Sum of the angles of a quadrilateral is 3600.
(2) A diagonals of a parallelogram divides it into two congruent triangles.
(3) In a parallelogram
(a) diagonals bisects each other.
(b) opposite angles are equal.
(c) opposite sides are equal
(4) Diagonals of a square bisects each other at right angles and are equal, and vice-
versa.
(5) A line through the mid-point of a side of a triangle parallel to another side bisects
the third side. (Mid point theorem)
(6) The line through the mid points of sides of a ∆║ to third side and half of it.
Section - A
Q.1 The figures obtained by joining the mid-points of the sides of a rhombus, taken in
order, is
(a) a square (b) a rhombus
(c) a parallelogram (d) a rectangle
Q.2 The diagonals AC and BD of a parallelogram ABCD intersect each other at the
point O, if ∟DAC = 320 and ∟AOB = 720
then ∟DBC is
(a) 320 (b) 240 (c) 400 (d) 630
Q.3 In a square ABCD, the diagonals AC and BD bisect at 0. Then ∆AOB is
(a) acute angled (b) right angled
(c) obtuse angled (d) equilateral
Q.4 ABCD is a rhombus such that ∟ACB = 400 then ∟ADB is
(a) 400 (b) 450 (c) 500 (d) 600
Q.5 A quadrilateral ABCD is a parallelogram if
(a) AD || BC (b) AB = CD
(c) AB = AD (d) ∟A = 600, ∟C =
600, ∟B = 1200
Q.6 Three angles of a quadrilateral are 600, 700 and 800. The fourth angle is
(a) 1500 (b) 1600 (c) 1400 (d) None of these
Section - B
Q.7 In the adjoining figure QR=RS
Find
Q.8 Prove that the sum of the four angles of a quadrilateral is 3600.
Q.9 Prove that the diagonals of a parallelogram bisects each other.
Q.10 The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the
quadrilateral.
Q.11 ABCD is a rectangle in which diagonal AC bisects ∟A as well as ∟C. Show that
ABCD is a square
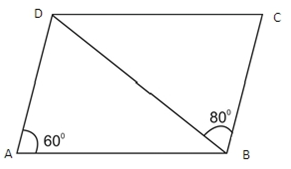
Q.12 In the adjoining figure, ABCD is a ||gm. If ∟DAB = 600 and ∟DBC = 800 .
Find
∟CDB and ∟ADB.
Section - C
Q.13 Prove that the line segment joining the mid-points of two sides of a triangle is
parallel to the third side.
Q.14 ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD
and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Q.15 Prove that the straight line joining the mid-points of the diagonals of a trapezium
is parallel to the parallel sides and is equal to half their difference.
Q.16 In the adjoining figure, D, E and F are mid-points of the sides BC, CA and AB of ∆ABC If AB = 4.3cm, BC = 5.6cm and AC = 3.5cm, find the perimeter of ∆EFD
Q.17 In a parallelogram ABCD, AP and CQ are drawn perpendiculars from vertices A
and C on diagonal BD. Prove that
Q.18 In a parallelogram ABCD, E and F are points on AB and CD such that AE = CE.
Prove that ED||BF.
Section - D
Q.19 If a line is parallel to the base of a trapezium and bisects one of the non-parallel
sides, then prove that it bisects either diagonal of the trapezium.
Q.20 AD is a median of
∆ABC and E is the mid-point of AD. BE Produced meets AC in
F. Prove that
AF = 1/3 AC.
Q.21 ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse
AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) CM =
MA = 1/2AB.
Q.22 Show that the bisectors of angles of a parallelogram form a rectangle.
Answers -
Q.1 (d) Rectangle
Q,2 (c) 400
Q.3 (b) Right angled
Q.4 (c) 500
Q.5 (d) ∟A = 600, ∟C = 600 , ∟B = 1200
Q.6 (a) 1500
Q. 7 ∟PSR = 1050


No comments:
Post a Comment